The infidelity of the theoretical protein backbone
Problems in protein simulations are often reduced to one of two categories:
- do we have a sufficiently accurate model of atomic interactions?
- have we sufficiently explored the conformational space of our proteins?
If you talk to molecular modellers, they will try to tell you the problem lies wholly in conformational sampling. It is an article of their faith that force-fields are good enough. Our erstwhile modeller can then claim that the problem lies not in software but in hardware. It's just that their computers are too slow to finish their simulations properly.
Well, I beg to differ. One major flaw in atomic force-fields, which has been swept under the carpet, is that atomic force-fields fail to properly model the protein backbone. And they've failed to do so, for decades.
Experimentalists have devoted much effort in understanding the protein backbone conformations, precisely because getting the backbone right has a disproportionate effect in determining the conformation of a protein from electron diffraction maps. The first thing crystallographers worry about is the Ramachandran plot of their derived structure.
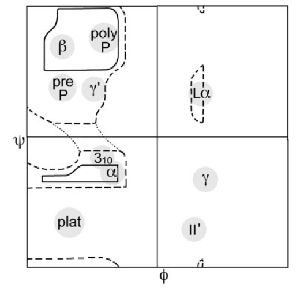
The Ramachandran plot is the allowed conformations of the φ/ψ angles of the protein backbone (I have a detailed introduction to the Ramachandran plot, which you can play with in my Ramachandran Plot Explorer)
Crystallographers have studied intensely the Ramachandran plot for decades. The original Ramachandran plot was first constructed in 1963 (Ramachandran et al 1963 JMB 7:95) which identified the two broad regions – the β-strand region in the top-left, and the α-helical region in the bottom-left:
Today's standard Ramachandran Plot is averaged over tens of thousands of high-resolution protein structures and provides a statistically controlled measurement of the protein backbone conformational space. Packages that evaluate this – PROCHECK and MOLPROBITY – are standard diagnostic tools. No crystallographer would dream of releasing a structure of a protein if their Ramachandran plot did not validate against these diagnostics.
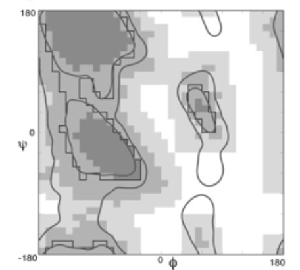
Here's Janet Thornton's classic PROCHECK map of the Ramachandran plot (Laskowski et al 1993 J App Crys 26:283). Here we can see the diagonal shape of the α-helical region, and the appearance of the semi-allowed regions, as well as an articulation of the left-handed α-helical regions:
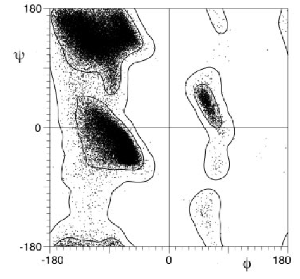
Probably the most used is Jane Richardon's MOLPROBITY describing the contour lines for the allowed regions of the Ramachandran plot (Lovell et al 2003 Proteins 50:437):
The fine structure in the standard Ramachandran plot identifies the conformations of the more complicated motifs in protein topology – β-hairpin turns, α-helical turns, γ-turns and β-bulges (disclosure – I worked on the Ramachandran plot for 8 years ~ 4 papers). These motifs require very specific backbone conformations in the Ramachandran plot in order to provide the correct intra-atomic interactions.
It is disheartening to learn that for decades, force-field developers have basically ignored all this experimental work on the protein backbone. Instead, our pointy-headed friends have turned to quantum-mechanical calculation of the energies and conformations of small amino-acids in vacuum, rather than to study the backbone conformations of, like, actual proteins. As a result, you will find that the Ramachandran plot calculated with classic force-fields completely misses out all the fine structure of the standard experimental Ramachandran plot.
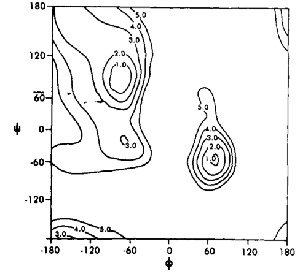
Here's an early force-field from 1984 (Weiner et al 1984 JACS 106:765), which doesn't even match the original 1963 Ramachandran calculation. Instead, the strong minimum corresponds to the formation of an internal hydrogen-bond – the γ-turn, which is rarely seen in real protein structures. This minimum however, appears in virtually any vacuum QM calculation. The right-handed α-region is in the wrong place:
This level of wrongness doesn't improve in 1995 (Cornell et al 1995 JACS 117:5179), by which time Peter Kollman had taken over force-field development for AMBER. This is particularly bad since by 1995, PROCHECK had already become de rigeur amongst crystallographers:
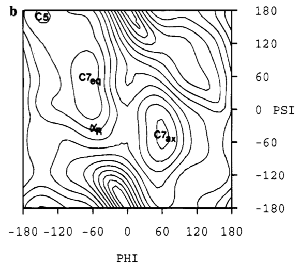
Meanwhile, Alexander MacKerrell and Martin Karplus (MacKerell et al 1998 J Phys Cem B 102:3586), who are plugging along with CHARMM, don't do much better:

One reason that force-field developers have not been so concerned about the crystallographic protein backbone, is that molecular-dynamics simulations have focused mainly on folded proteins. In folded conformations, many mutually reinforcing intra-molecular interactions in the compact folded state can compensate for the poor modelling of the backbone.
However, if the simulation involves any kind of disorder in the protein chain – loops, peptides, and protein folding – the simulation will crap out. Wait, you say, but force-field developers do test their force-fields against flexible backbones. If you read their papers carefully though, you will find that these test don't go beyond calculating α-helical propensities versus β-strand propensities. Arguably a more realistic challenge would be to reproduce complicated motifs such as β-hairpin turns, γ-turns, or α-helical turns. These turns have very well-defined conformations. That no such molecular-dynamics model can reproduce these turns at any level of accuracy really needs to be mentioned.
If I might hazard a guess to why ab initio protein folding using "physically realistic" models has failed so badly, I would hazard that the crappy modelling of the protein backbone might play a part. Taking the "nucleus" view of protein folding, the formation of turns and kinks are crucial in defining the tertiary structure. The reason is that it is the reversal of the chain generated by turns that bring the correct pieces of secondary structure together. As well, β-bulges and helix caps control the extent of secondary structure. These are typically generated by the fine structure regions of the Ramachandran plot. If your model force-field can't generate all the fine structure of the observed Ramachandran plot, you will never get these turns and bulges in the right place, and thus miss out on the correct tertiary structure.
I think one of the main reason that David Baker's Rosetta program for protein-folding has been so successful was that he found a way to overcome the crappy force-field modelling of the backbone. Rather than try to fix a broken thing, he bypassed the problem altogether by constructing a library of statistically probable local fragment conformations (Bystroff 1998 JMB 281:565). In Rosetta, certain high scoring short sequences are assigned φ/ψ angles direct from the fragment library. These are based on crystal structures, and not on some artificially wrong force-field. By identifying correct chain reversals from the very beginning, Rosetta searches in the right valleys in the conformational space.
I am happy though, to report that after decades of mis-placed faith in quantum-mechanical purity, force-field developers have been dashed back onto the beach of experimental data. Recent updates of force-fields have started to incorporate experimental corrections to the backbone force-field parameters.
Here's the popular CHARMM 22 forcefield (C22) is shown on the left, giving a crappy Ramachandran plot. In 2004, Alexander MacKerell added a grid-based φ/ψ term (CMAP) to the CHARMM 22 (C22) force field (Mackerell 2004 J Comput Chem 25:1584). The corrected CMAP Ramachandran plot (on the right) shows that the grid-based correction turns a very crappy Ramachandran plot into something that at least might look acceptable to a crysallographer:

In a similar vein, Carlos Simmerling added some experimental tweaks to AMBER in 2006 (Hornak et al., 2006, 65:712). Compared to the crystallographer's PDB (left), the tweaked AMBER Ramachandran plot (right) fixes some things but is still poor in the α-helical region:

The irony is that as the force-field developers have turned to experiment rather than rely on quantum chemistry calculations, quantum chemists are starting to get a grip on the Ramachandran plot. A quantum mechanical calculation of the alanine dipeptide using DFT with a sophisticated solvent model (Tsai et al., 2009, J Phys chem B, 113:309), gives the first decent ab initio calculation of the Ramachandran plot:

As we're starting to have success in folding proteins using unbiased long-time MD (Shaw et al 2010 Science 330:341), some might think that our backbone atrocities have now been eliminated. But as these proteins have very simple topologies (WW domain), the turns don't need to be so well defined. I'm guessing this won't scale to more complicated topologies. Large topologies such as the β-sheets of serpins will require perfect modelling of the intervening β-hairpin, which still can't be done.
I have long held the view that until we can reproduce the local fragments of Rosetta in unbiased MD with some future force-field, we cannot say that we have modelled the backbone properly. Until then, we will continue to suffer the bloated claims of our pointy-headed force-field friends.