The Mysterious Regions of the Ramachandran Plot








G.N. Ramachandran was one of the gods of structural biology. He solved one of the first protein fibre structures, the triple-coil of collagen, and in the process, created powerful new tools for analyzing protein conformations. The most important tool is the one that bears his name, the Ramachandran plot (Ramachandran, 1963, JMB 7:99) and virtually all tools that analyze protein conformations descend from the Ramachandran Plot (look at it using my protein viewer, the Ramachandran Plot Explorer for mac/win/linux platforms).
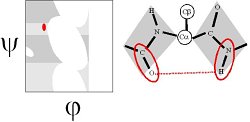
Ramachandran realized that, if the peptide plane is planar and trans, then the conformation of the protein backbone can be described by the φ and ψ dihedral angles of the protein backbone.
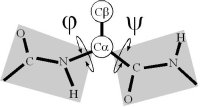
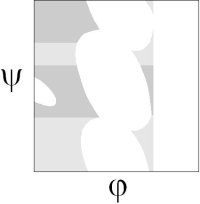
The original analysis by Ramachandran of the stereo-chemistry of the protein backbone was as elegant as it was simple. In a tour de force calculation (carried out by hand in the ago before computers), he analyzed all the steric clashes in the protein backbone as a function of φ-ψ. He showed that the allowed values of φ-ψ (gray) broke into broadly three regions, which are known as α, αL and β.
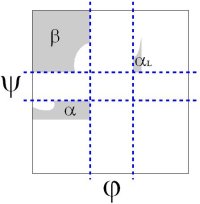
The backbone conformation of these regions corresponds to different secondary structure, the α-helix, the αleft-helix and the β-sheet.
The Regions of the Ramachandran Plot in Hi-res Structures
Nevertheless, there are small but significant differences between the original steric map of the Ramachandran plot to high-resolution data
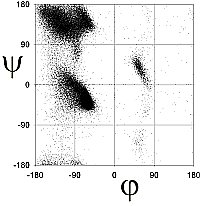
Richardson and co-workers analyzed this data to determine the exact limits of the Ramachandran plot (Word, JMB, 199, 285:1711). They calculated the 98% and 99.98% percentile contour lines, showing interesting structure outside the clustered regions.
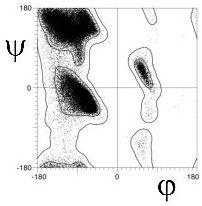
There are 5 well-defined clusters in the Ramachandran plot: βS, βP, α, αL and γ regions, each representing a distinct backbone conformation (Ho et. al, 2003, Pro Sci 12:2508).
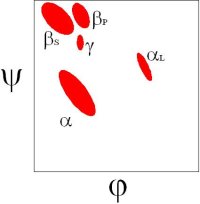
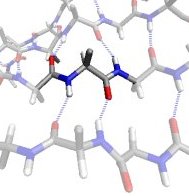
In the βS region, the CO and NH dipoles are parallel, which can both form hydrogen bonds with the same cross-strand neighbouring residue in a β-sheet.
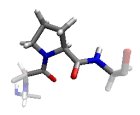
In the βP region, the CO and NH groups are almost perpendicular and the Ci-1...O interaction is optimized. Proline preferably adopts this conformation.
In the α region, the CO and NH dipoles are antiparallel, which can form hydrogen bonds in opposite directions in a helix. The orientation of the CO and NH dipoles affects whether an α-helix, π-helix, or 310 helix is formed.
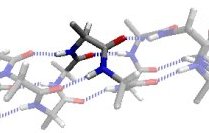
The αL region is the mirror image of the α region, except for a steric clash between the O and Cβ atoms.
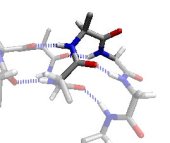
In the γ region, the outer CO and NH dipoles (that really belong to the two neighbouring residues) form a very distorted hydrogen bond. This is known as a γ-turn. Revised Steric Interactions in the Ramachandran Plot
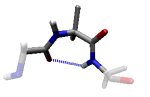
Revised Interactions that induce the clustered regions
The hi-res Ramachandran Plot clearly differs from the original map calculated by Ramachandran. Ho and co-workers (2003, Pro Sci 12:2508) re-analyzed the interactions of the Ramachandran plot by using the statistical distributions from the hi-res structures as a guide. They found that certain steric interactions in the original Ramachandran analysis, did not repel. This was due to hithero unsuspected electrostatic interactions.
By ignoring these steric interactions, Ho and co-workers created a revised steric map, where revised allowed regions (gray) gave a better fit to the 98% region of the Richardson's hi-res Ramachandran plot:
Then they used electrostatics to model the interaction between the inner CO and NH dipoles. They found that the electrostatic-dipole interaction pick out the βS, α and αL regions as energy minima. The dipole interaction aligns the CO and NH in either the parallel and antiparallel orientations.
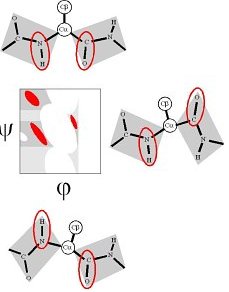
The βP region is induced by the COi-1...CO dipole-dipole interaction (Macculum, 1995, JMB 248:274).
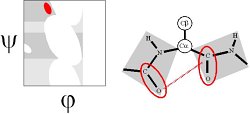
The γ region is induced by the COi-1...NHi+1 dipole-dipole interaction. This can be thought of a distorted hydrogen bond and thus constitutes a γ-turn (Milner-White, 1990, JMB 216:386). It is the vacuum energy minimum of the alanine dipeptide.