How to build a cathedral door out of 456 proteins

Bioinformatics has always made a dirty little promise that if you feed it enough data then by a little wave of the magic wand of algorithm, your voluminous pile of experimental data will be transformed into a valuable nugget of physical insight. Of course, the practice rarely hits that particular grace note. But a recent Nature paper has managed that very rare feat.

I am talking about the tour-de-force calculation [1] from the Andrej Sali lab of the molecular structure of the entire nuclear pore complex [2], the door-way to the nucleus.

This complex is made up of 456 proteins and weighs in at 50 000 000 Da. In the world of protein complexes, this is a big motherfucker. Not only is this a massive complex, but it is heteregenous. Other massive complexes have been solved – the virus capsid comes to mind – but they possess high order symmetries and very few components, which dramatically reduce the amount of information needed to solve the structure. Not so for the nuclear pore complex. There are over 30 types of proteins and the entire structure has only a eight-fold symmetry in the form of a massive wheel. These puny symmetric constraints won't take you very far.

The central idea is this: can we convert every piece of experimental data about the interactions of the proteins into geometry? A simple idea conceptually, but a tremendously difficult task when taken in all its technical gore. Working in the same building, I know that the main author of the work, Frank Alber, has been moving mountains over the last 8 years to make the system converge.

Just the variety of experimental data is enough to make a computational biologist cry – ultracentrifugation, immunoblotting, affinity purification, electron microscopy, immuno-electron microscopy, fractionation. All of these have to be turned into well-behaved geometric constraints where the different geometric constraints apply on completely different size scales. For instance, centrifugation data gets you the shape of the protein, immuno-microscopy localizes the protein in the complex, and affinity purification puts distance constraints between proteins.

Internally, the system represents the nuclear core complex simultaneously at 9 different levels of detail including a domain level, a protein level, a protein-complex level, and various levels of symmetry including the eight-fold symmetry of the spoke. At different levels, the elements are represented as spheres or string of spheres or space-filling blobs. Anyone who's done any kind of modeling will appreciate the complexities involved in mixing representational levels. It's hard enough sticking to one level of approximation, let alone mixing up to 9 very different inter-penetrating representations at the same time.

One of the many clever ideas in this paper is the idea of the conditional spatial constraint. The problem is this: in protein affinity experiments, you can determine interactions between two proteins, but it's not at all clear how to turn this into a constraint. First, you don't know which two proteins in the complex because many of the proteins have multiple copies. Second, you don't know which domains are interacting. Third, you don't if it's actually mediated by a third protein in a complex. If you have a complex with 4 proteins (1 yellow protein with 3 domains, 2 green proteins with 2 domains, 1 orange protein with two domains and 1 blue protein with 1 domain) then the protein-protein interaction info could arise from any of these interactions:

However, the idea of the conditional constraint is to parse all the possible constraints consistent with the protein-protein assay and choose the weakest set of constraints:

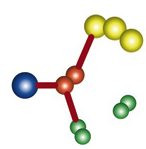
This allows the search as minimally impeded by the constraint as possible in order to make the search more robust. Everything is churned through a huge monte-carlo search until a single, inexorable solution rises out of the slop of calculation.

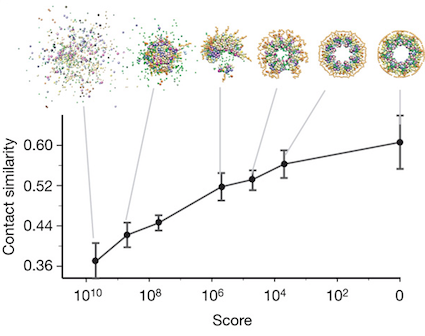
Once you look at the final structure, the spatial arrangement of the 456 proteins that make up the nuclear pore complex, you realize that this is the kind of result that computational biologists dream about. The architecture of the nuclear core complex – and here, you can really use the word architecture without hyperbole – immediately rationalizes the function and position of all the proteins in the nuclear core complex.

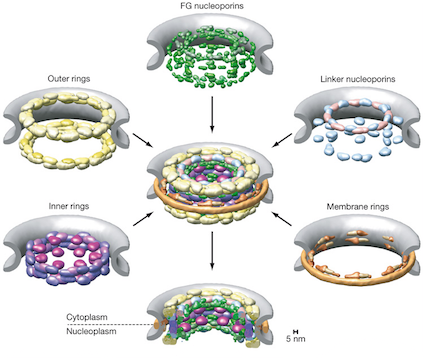
The assembly tells you exactly which protein interacts with which other protein, and places each protein exactly in the context of the cell – membrane or cytoplasm or in the rim, or facing the pore. When computation transmutes crude experimental data into an irrefutable physical model, abstract algorithms touches the real.

[1]: Alber et al (2007) Determining the architectures of macromolecular assemblies. Nature. 450:683-94.

[2]: Alber et al. (2007) The molecular architecture of the nuclear pore complex. Nature. 450: 695-701.