How efficient is Molecular Dynamics?

Those of you who do computational biology may sometimes run across the big O(n) notation of computer science, which measures how efficient an algorithm is. For instance O(n) = log n is good, where n is a rough measure of the size of your imput, and the calculation takes log n number of steps. If O(n) is a polynomial, such as O(n)=n³ your algorithm won't scale too well with the size of the input.

So how does a general Molecular Dynamics simulations do? Well I finished a bunch of simulations recently, simulating a whole range of proteins, and I realized I could compare how long it took for different proteins and calculate roughly the efficiency of Molecular Dynamics as a function of protein size. Technically, I performed a 10 ps simulation using AMBER with an implicit Generalized-Born/Surface-Area solvent.

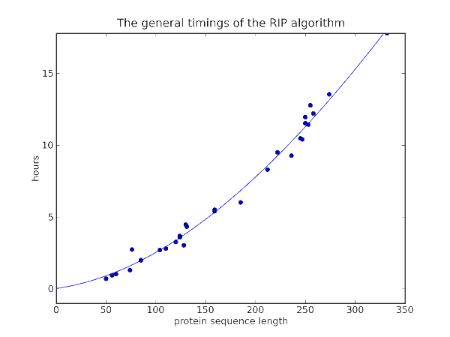
In order to find the O(n) of AMBER, I did a log-log analysis:

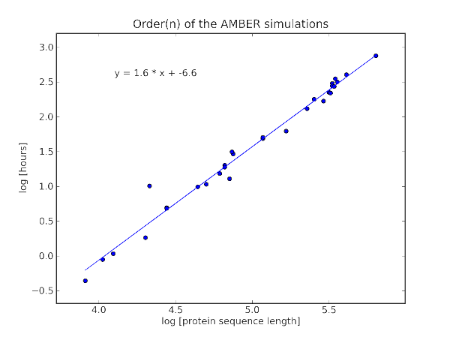
which shows that

    Simulation time ∝ (protein sequence length)^1.6

Naively, you'd suppose that at each step, we'd need to consider the interaction of every atom to every atom, giving roughly (protein sequence length)². But there are all sorts of tricks to skip some of the calculation as some amino acids are far away and unlikely to interact. To conclude, AMBER is efficient in so far as it can lop 0.4 off the efficiency of the expected O(N) of the calculation.